טור לורן

בוקר טוב הודיה!!!

כמו שאני תמיד אומר לכולם-הכי חשוב לקבל בטחון. הפקל מכיל את כל הניסוחים שיכןלים להופיע במבחן וצריך לשלוט בכולם כמו שסיפרתי לך בהודעות קודמות, לדעת סיפור עם עלילה טובה עם כל החלומות שלו והמשפטים הפלאשבקים מהסדרה הכל. בשאלות האלה עם הניסוחים "מתכנס בנקודה כלשהי" שזה נתון, זה ניסוח שגם מופיע רצלי בפקל בחלק של טורים בפרק הטורים שם היה לי ניסוח של "מתכנס בZ=0" אבל זה בדיקו אותו ניסוח. באותט הקשר, התמונה ששלחתי לך אתמול, התמונה העדכנית, ראית הוצאתי שם 2i החוצה ולא הוצאתי את Z פחות i החוצה במכנה, למה דווקא הוצאתי אותי ? כי רציתי שתחום ההתכנסות ש טור לורן ייצא שיכלול את התחום הנתון בשאלה, כי מעגל ברדיוס 2 עם מרכז i  באמת מכיל מעגל עם מרכז i ורדיוס 1 שזה היה התחום הנתון.

בחזרה לשאלה שלנו-קודם כל הכבוד ששמת לב לטריק של לחשב עם נוסחת קושי, נגיד בפרק השארית בתרגיל שהיה שם תרגיל לחשב מקדם של טור של פונקציית קוטגנס שם גם התחום היה נתון וגם זה היה פונקציה שבלתי אפשרי לחשב טור לכו ישר הלכנו לחישוב המקדם דרך נוסחת האינטגרל של קושי משם שארית.

לגבי הדרך שלך-קודם כל כל מה שאת צריכה לעשות אם משתמשת בה(שהיא באמת מדהימה בפני עצמה אבל יש לי מה להגיד על זה ומעולה ששמת לב עליה כי זה מציל בהרבה שאלות בחלום האמריקאי בפקל יש לי תרגיל אפיול יותר קשה עם פונקציה עם לוג שגם שם יותר קל בדרך של אינטגרל קושי ואנ משתמש שם דווקא בה)- העיקר זה פשוט לבחור מסילה גאמה כלשהי שמוכלת בתחום שלא מכיל את הנקודות הסנגולריות אבל התחום הזה כן מכיל את הנקודה שהם אמרו שבתחום. נגיד היינו בוחרים את התחום |Z|>שורש 2(למה אני יודע את זה? תכף תראי בתמונות חח יכול גם להיות גדול משתיים גדול משלוש גדול מארבע כבר לא כי רדיוס של 4 יותר גדול מרדיוס של 2+3i) זה תחום שאכן מכיל את הנקודה שהשאלה רצתה ולא מכיל את הסנגולריות. עכשיו תציירי לעצמך גאמה סגורה סתם קשקוש של משהו סגור בתחום הזה, את רואה שהגאמה הזאת מכילה ב-INTERIOR שלה את כל הסנגולריות אז זה למה החישוב שלך נכון אבל היה לך מזל זה מה שאני אומר. שוב כל הכבוד ששמת לב לטריק הזה-אני משתמש בחישוב מקדם עם אינטגרל בכל מיני מקומות-גם חלום אמריקאי יש שם איזו שאלה עם לוג ומקדם יותר קשה מזאת וגם מה שאמרתי עם קוטגנס בסוף סרטון ראשון שארית. הוא באמת מציל חיים במלא מקומות וגם כאן הוא הציל אותנו. אז הדרך שלך מאוד לגיטימית, כי אני לוקח את התחום נגיד שאמרתי שמכיל גם את הנקודה המבוקשת ולא מכיל את הסנגולריות הגדול משורש 2 הזה, גם גדול משתיים יכול לעבוד, גם גדול משלוש יכול לעבוד העיקר שיכיך את הנקודה המבוקשת לא את הסנגולריות ובתחום הזה את מציירת סתם קשקוש של מסילה גאמה סגורה ואז הפנים שלה מכיל את כל הבעיות כמו שקורה בסרטון של פונקציה קדומה ששם התחום נגיד לא הכיל לנו את הראשית אבל הגאמה עצמה מהתחום כן הכילה את הראשית. אותו דבר כאן רק עם 4 נקודות, אבל מה שעשית הוא נכון רק בגלל שלא נתון תחום זה היה מסוכן אבל היית מדהימה יש הרבה מאוד שאלות שזה קריטי ואני מאוד שמח ששמת לב לזה ישר להזכר באינטגרל שם. כמו שאמרתי נראה לי בהודעה הזאת הרבה פעמים כי אני אוהב לכתוב לאנשים כל מה שהראש שלי  שאני מדבר על מרוכבות חושב כאילו שאני כותב על מרוכבות אני מדמיין כאילו אני בשיחה פיקנטית-הרתגילים מהפקל של קוטגנס מסרטון ראשון שארית הפונקציה עם לוג מהחלום האמריקאי בדיוק עושים אותה טכניקה כמו שאת עשית.

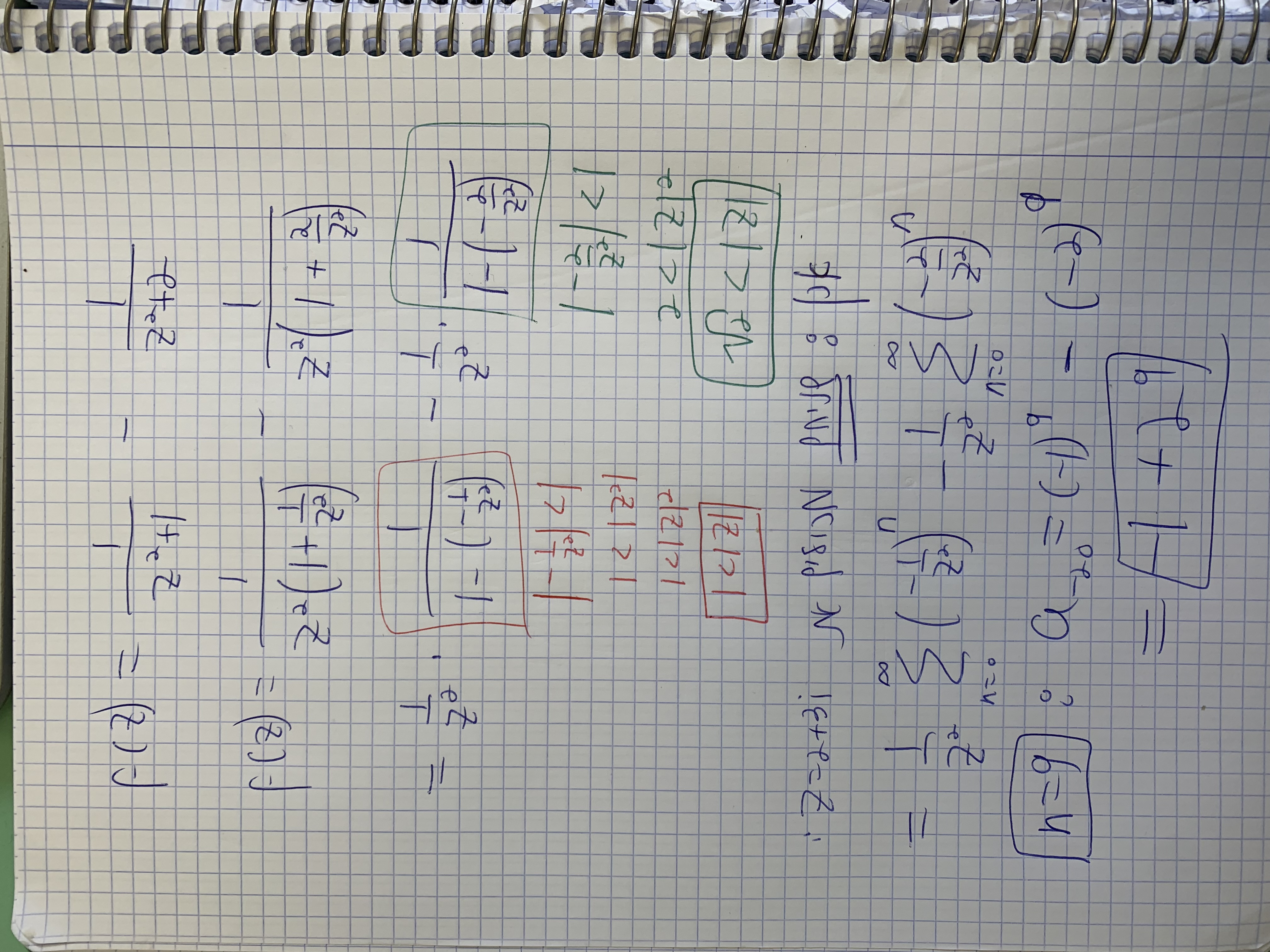
לחלופין, הדרך השנייה, שאת רואה את הניסוח הקלאסי הזה כמו שאני מראה בפרק הטורים(זה למה חשוב לזכור כל סיפור אפיול אם הוא נראה לא קשור לעלילה להיות מוכנים לכל סיפור מהפקל), שאת רואה את הניסוח "מתכנס בנקודה ABC" זה ניסוח בעלילה שממש מרמז על לפתח דווקא לטור פה ולא לעשות דרך קושי , יש תרגילים אחרים כמו ההוא עם הקוטגנס בשארית ששם היינו חייבים קושי גם התחום שם היה נתון אז זה קבע לנו את המסילה וגם זה היה פונקציה מואד מסובכת ולא ראלי לחשב שם טור. אבל כאן הניסוח הזה של "מתכנס בנקודה.." זה חלק בעלילה שאומר לך לפתח לטור כמו שאני עושה בתרגילים דומים בפקל. מצרף לך פתרון: שימי לב איך כאן הוא יותר קצר , צריך לשים לב באיזה משתי הדרכים עדיף להשתמש, אבל שוב יש מקרים שרק הדרך של האינטגרל לחישוב מקדם היא ראלית לחשב טור בלתי אפשרי, אבל בדוגמה הזאת  בגלל הניסוח הפסיכולוגי שסיפרתי זה אומר טור מהר יותר אבל גם שלך מהסיבה שהסברתי פשוט פיקנטית, מעלפת ומטורפת ונותנת את הכבוד הראוי לאלופים שנושאים בדמם את טיפ האפסים לאלופים. עדיין טור יותר קצר פה חח

לסיכום-פשוט שאת עושה עם אינטגרל להזהר איזו מסילה את בוחרת כי המסילה שבוחרים הגאמה זה קובע לנו מה יהיה בINTERIOR  זה לא סתם משהו שולי, ברגע שיש לי תחום אני יודע שהגאמה חיה בתוכו אז אני סתם מצייר קשקוש של גאמה סגורה שרירותית בתחום כמו בפרק של פונקציה קדומה בסרטון שם.

אבל שוב ממש בסדר גם עם אינטגרל כאן, רק טוב שהבנת למה באמת המסילה הכילה בINTERIOR שלה את כל הנקודות הסנגולריות ולא רק חלק מהן, כשהתחום נתון מפורשות כמו בשלאות אחרות יותר קל לצייר גאמה שרירותית סגורה שם ולראות מה יש בפנים שלה, כי נגיד הגאמה לא הייתה מכילה את כל הנקודות אז הייתה מקבלת תוצאה שונה אבל כאן היא חייבת להכיל בפנים שלה את כל הבעיות הסנגולריות, כי התחום נגיד זה טבעת חיצונית שמכילה את הנקודה המבוקשת ולא את הסנגולריות

עוד אינטאוציה: בטור לורן תחום התכנסות הוא תמיד טבעת!!! זה למה באמריקאי היה מספיק פשוט לצייר לעצמך טבעת רלוונטית שמכילה את הנקודה המבוקשת ולא את הסנגולריות

אז מה שעשית סופר לגיטימי- פשוט לזכור שתחום התכנסות בטור לורן הוא טבעת וכאן זה טור לורן נתון ואז זה פחות מסוכן

באמריקאית אפשר גם לרמות את סתם מציירת טבעת שלא תכיל את הבעיות וכן תכיל את שתיים פלוס שלוש איי כי את יודעת בתת מודע שטור לורן תחום תכנסות חייב להיות טבעת, ולפי השאלה זה חייב להיות טבעת שמכילה את הנקודה הרצוייה ולא מכילה את הסנגולריות

מצטער על אורך ההודעות, שאני שולח אותן אני אפילו לא חושב מה אני כותב אני מדמיין שאני כותב סיפור חחח מקליד מהר ומה שיוצא יוצא

עוד משוה בשיטה של הטורים : להזהר איזה N מציבים!!!

אני הצבתי כאן N=9 כי זה מה שהביא לי סהכ את הבחזקת מינוס עשרים לא תמיד החזקה מתאימה לאינדקס הרצוי הכל תלוי במה שקבלנו בטור , זה רק לראות איזה מספר להציב כדי לקבל את הבחזקת מינוס 20 אפילו לפתור בצד משוואה

2Nּּ+2=20

איך ידעתי מה להוציא החוצה במכנה בתמונה בירוק ובאדום? את פשוט מנסה את שתי האופציות בכל מכנה ורואה איזה מםה מביא לך תחום שמכיל את הנקודה שתיים פלוס שלוש איי בדיוק כמו הפקל רק ששם הוצאנו במכנה למטה ככה שהטורה יכיל את הראשית ובשאלה אחרת נקודה אחרת שהייתה שם

4 החברים הכי וטובין- טור גאומטרי כתלות במה שאנחנו מוציאים אנחנו מקבלים תחום התכנסות שונה

הא ושכחתי לצרף לך- פירוק לשברים חלקיים שלב מקדים אם עושה עם טור

הא ועוד משהו-הפיתוו לורן פה הוא אכן סביב אפס לפי הנתון, כלומר זה למה זה טבעת ממורכזת סביב הראשית

המחשה ווזיואלית לגאמה לאחרת לקיחת תחום D חיצוני לטבעת:

גאמה אכן נמצאת תחום התכנסות שזה טבעת עם רידוס פנימי נגיד שורש שתיים או נגיד שתיים או נגיד שלוש או לא נגיד ארבע, והגאמה הזאת מוכלת בתחום שלנו מכילה בINTERIORBשלה את הנקודה הירוקה שתיים פלוס שלוש איי , ובנוסף הINTERIOR שלה מכילה את כל הסנגולריות זה למה החישוב שלך נכון עם כל הנקוודת הINTERIOR זה מה שחשוב מילה שאני אותה כל הזמן עם DOUBLE R בכל הפקל

רדיס חיצוני של הטבעת נגיד יכול להיות אינסוף הוא גם יכול להיות 17777777777777777

או 28888 העיקר משהו גדול מרדיוס הנקודה הירוקה, כלומר הרדיוס הפנימי של הטבעת קטן מהנקודה הירוקה והרדיוס החיצוני גדול מהנקודה הירוקה פשוט אינסוף בחיצוני הכי נוח אבל כל רדיוס חיצוני שגדול מירוקה מעולה, כלומר גדול משורש 13, ורדיוס פנימי שיהיה קטן משורש 13, אבל לא קטן מדי במאל באמירקאי לא יעלו עלייך אם תקחי קטן מדי כי לפי מה שהארתי פורמלית בטורים צריך יותר גדול משורש 2 רדיוס פנימי אבל גם אם סתם היית מציירת טבעת זה כאן אמריקאי אז הם בחיים לא ידעו, אבל ריגורוזית רדיוס פנימי קטן משורש 13 וגדול משורש שתיים, וחיצוני גדול משורש 13 נגיד אינסןף