מרוכבות- שימוש למשפט השארית פונ' קדומה

שלום הודיה

אם אני פתרתי את האינטגרל באמצעות קושי במקום שארית זה אומר שאני רשמתי אותו בצורה של "אנליטי חלקי מבנה מאוד ספציפי של z פחות z0 בחזקת N+1".  לפי מה שלמדנו ב"העאאאAAשיטה" כאשר אני רוצה לגלות סווג סנגולריות אנחנו כמעט תמיד נפתח לטור רק כאשר בלב אנחנו יודעים שזה עיקרי לפי הרמזים שאמרתי שם, למרות שהייתה שם דוגמה מאוד טובה ממבחן שאני פתרתי בשתי הדרכים כי ההעעAאאAשיטה הייתה ארוכה אבל גם עבדה וכמובן ששווה את העשר נקודות. בתרגיל הזה ששאלת לא צריך לפתח לטור כאן כי אין רמז לעיקרי כמו הדוגמאות האחרות שראית בסרטון ששם היה לך סינוס של אחד חלקי Z קוסינוס של אחד חלקי Z דברים כאלה, כאן זה יוצא שם קוטב מסדר ראשון(קוטב פשוט) ואז מציבה בנוסחה של תרומה של קוטב בשארית בלי טורים. לשים לב שבקושי הנוסחה מדברת על המונה ובשארית אני מסתכל על כל הפונקציה כמכלול לא רק על המונה בנוסחה של תרומה של קוטב. לחשב A_-1 זה תמיד נכון אבל אנחנו עושים את זה רק כאשר בלב אנחנו יודעים שזה עיקרי כמו שלמדנו בסווג סנגורליות וכמו שראית בתרגילים אחרים בסרטון פונקציה קדומה וגם תראי בהמשך הפרק ב"מקרה מיוחד שימוש 3 שארית". בשארית אפילו לא צריך להגיד במבחן שאת יודעת בלב שזה עיקרי כי לא בקשו לסווג את רק יודעת את זה בנפש וזה למה מפתחת ומוצאת את המקדם.

אולי זה בלבל אותך כי ראית עד כאן שכל הסרטון אני מפתח לטור, אבל זה כי בעיקרית אין לנו בררה אין לנו נוסחה מוכנה כמו בקוטב אז חייבים למצוא A_-1. בסליקה תרומה היא תמיד אפס. אבל עיקרית חייבים טור.

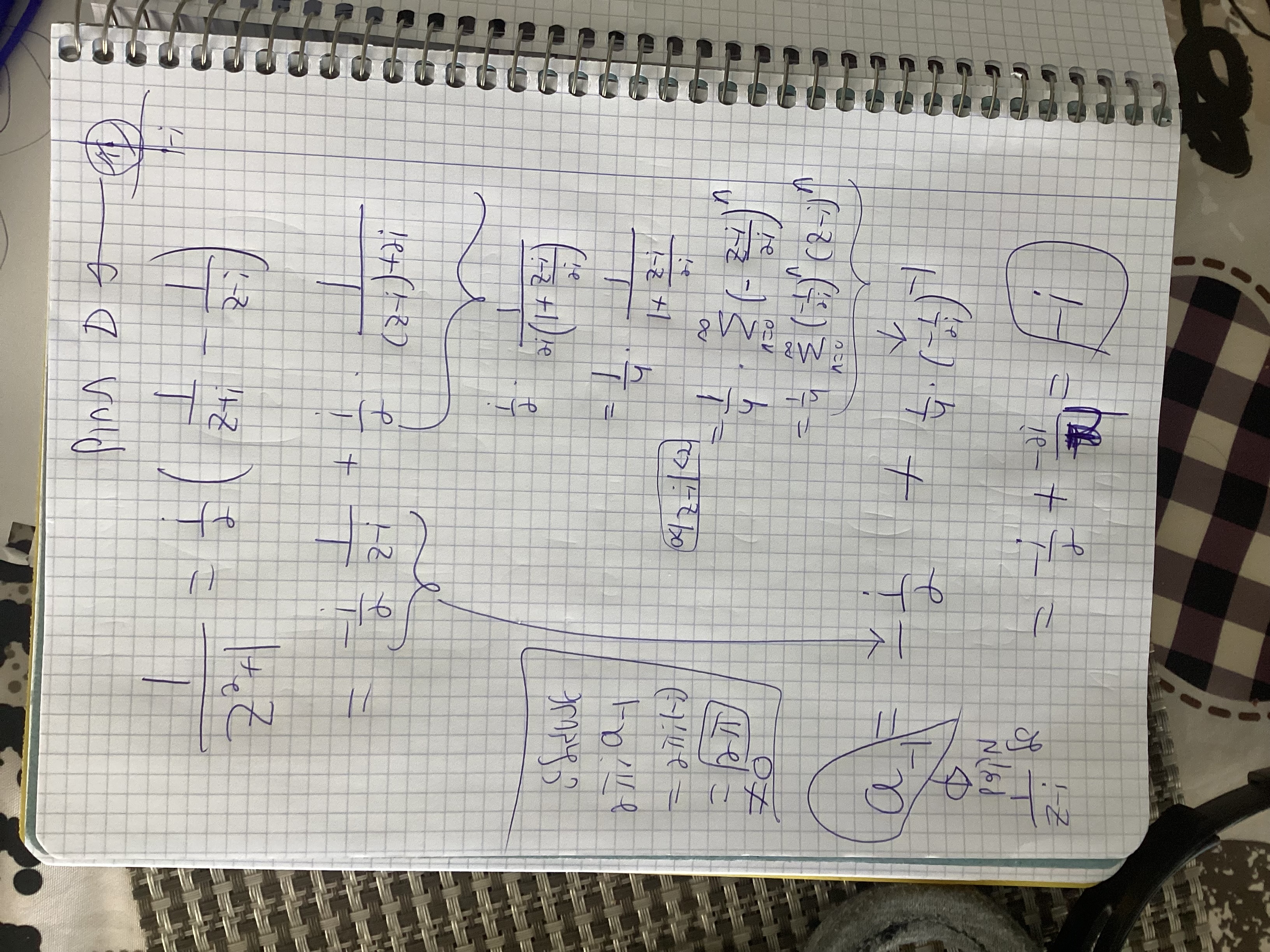
למרות הכל, בגלל שכאן הפונקציה היא רק אחד חלקי Z^2+1 אפשר לעשות פרוק לשברים חלקיים ולמצוא את המקדם בפיתוח של טור סביב Z=i(אם רוצה אראה לך כמו שעשיתי בפרק הטורים אני עושה הרבה כאלה שם כי נקודת הפיתוח נקבעת לפי מרכז המעגל בתחום שלנו בתרגיל) , אבל זה לא באמת GOOD PRACTICE כי מה אם נגיד היה אחד חלקי Z^5+2Z^3+78Z+9? לא היינו באמת מפתחים לטור.

אז לסיכום-לחשב כאן רגיל בלי טורים, אם מאוד רוצה כותב לך עם טורים אבל אין סיבה שנעשה את זה במבחן אם יש לנו נוסחה מוכנה לקוטב,צריך לפתח סביב נקודת מרכז המעגל ולראות מה המקדם של אחד חלקי Z-i כמו שאני עושה בפרק על טורים.

כאן הדרך המומלצת אם עושה עם שארית זה קודם כל לפי הההעעAAאאשיטה לראות שזה קוטב מסדר ראשון ואז ישר להציב בנוסחה של תרומה של קוטב ואז תשובה סופית באינגטרל לפי שארית זה שתי פאיי איי כפול סכום התרומות ובמקרה הזה יש רק תרומה אחת כי במקרה ששאלת שעשיתי עם קושי זה כי הייתה רק בעיה אחת כלומר מינוס i לא בתחום.

מעתיק משפט מהודעה קודמת שוב כי הוא חשוב

אולי זה בלבל אותך כי ראית עד כאן שכל הסרטון אני מפתח לטור, אבל זה כי בעיקרית אין לנו בררה אין לנו נוסחה מוכנה כמו בקוטב אז חייבים למצוא A_-1. בסליקה תרומה היא תמיד אפס. אבל עיקרית חייבים טור.

איך מרגישה עם זה?

בסווג סנגולריות אני רק מפתח לטור כאשר בלב אני יודע שזה עיקרי , חוץ מדוגמה אחת ממש טובה שם שגם םיתחתי לטור וגם פתרתי עם "הההעעשיטה". כשיודעים בלב שזה לא עיקרי כי אין את הרמזים של עיקרי, נעשה עם הההההשיטה למרות שגם שם אפשר טור כמו בדגומה אחת שאמרתי שעשיתי עם שתי השיטות.

אותו דבר בשארית, אנחנו 99% מהפעמים מפתחים לטור שבלב אנחנו יודעים שזה עיקרית הבעיה, אחרת ישר הההעעשיטה למרות שתמיד אפשר טור כמו שאני עושה בדוגמה אחת מיוחדת בסווג סנגולריות או בכללי שאנחנו מרגישים שזה עיקרי

אבל מה שבפועל יקרה לך במשפט השארית-את תעשי טור רק שהלב אומר לך שזה עיקרית , אחרת הההעעשיטה והצבה בנוסחה של קוטב(כי סליקה לפי ההשיטה גם נוכל לגלות ואז אומרים תרומה שלו אפס במשפט השארית). A_-1 הוא תמיד נכון, אבל אנחנו לא תמיד רוצים לחשב אותו , בבעיות שהם קטבים יש לנו נוסחה מוכנה בעיקרית אין לנו נוסחה מוכנה זה למה עושים A_-1. A_-1 זה טוב גם לשאלה תאורטית כי זה משהו כללי כמו שאני עושה בדוגמה אחרת בסרטון של קדומה.

טוב די חזרתי על עצמי אבל אם זה הבהיר את הנקודה אז אני שמח

להמשיך לשלוט בכל הטריקים זה מה שיביא לך את הבטחון, אם רוצה את הפתרון עם טורים תגידי או שתראי מה עשיתי בפרק טורים איך אני עשיתי שפ פיתוח טור סביב נקודות שהן לא אפס. הביטוי 1 חלקי Z-i הוא כבר מפותח סביב i לא צריכים לגעת בו בביטוי אחד חלקי Z+i צריל לטפל. אם אתה בפרק 6 זה אומר שאת לקראת הסוף כל הכבוד, אחרי שמסיימת לחזור על הכל כמו לקרוא ספר טוב וזה יעזור לך להטמין את כל החלומות והטריקים שלהם בצורה הרבה יותר חזקה. 

מאמיו בך,

אלחנדרו

הפיתוח לטור הוא סביב נקודת הפיתוח סביב הסנגולריות לא אפס .

צירפתי לך גם עם טורים לצורך תרגול בטורים אבל במבחן יותר מהר הההעעעשיטה פלוס הצבה בנוסחה של תרומת קוטב בכל יום בשבוע ובכל שעה בשבוע

הפיתוח הוא סביב הבעיה שאנחנו מתעניינים בה, i 

מעבר ראשון בתמונה פירוק שברים חלקיים אחרי זה מה שבאמת חשוב לנו זה לראות מי המקדמים של אחד חלקי Z-i

בשאלות הקודמות בעיקריות בקדומה זה היה שווה לפיתוח סביב אפס כי הבעיה הייתה אפס ולא במקום אחר, וזה גם מה שיהיה במבחן וגם אם זהלא סביב אפס , אז במבחן בשאלות של שארית לא יביאו לכם עיקרית שהיא לא באפס(בשאלות סווג כן ושם אני כן מראה עיקריות שלא באפס), במבחן כן מביאים כמובן בשאלות שארית קטבים וסליקה שהן לא באפס כמו שאני מראה בסרטונים

כי Z-i בחזקת מינוס אחד זה אחד חלקי Z-i אז זה למה זה  המקדם המעניין, במבחן עדיין תעשי בדרך של תרומת קוטב ולא טור בתרגיל הזה למרות שהראתי לך שתרגישי גם בטוחה בזה

להסתכל על התמונה המעודכנת שימי לב הביטוי השני אסור להציב בו N=-1 כי זה מתחיל מ-N=0 ואז יוצא בדיוק כמו הסרטון, מה שקרה אצלך זה שעשית פיתוח סביב אפס ולא סביב i זה למה יצא לך שונה אבל לא נורא אלופה ככה לומדים!

אם Z-i  היה במכנה סיפור אחר אבל הוא במונה בתוך הטור שקבלנו כי רצינו שתחום ההתכנסות של הטור יכלול את התחום הנתון בשאלה זה למה זה הטור, אני מפתח כאלב בפרק על טורים. רק צירפתי לך את זה כי רצית דרך טורים אבל במבחן כדי שתקבלי את ה-90-100 לא לבזבז על זה זמן ולעשות במקום כמו שאמרתי עם קוטב פשוט נוסחה

תמשיכי לשנן את כל הסרטונים ושיהיה מלא בהצלחה שמחתי לעזור ומקווה שעכשיו יותר ברור