איך יכול להיות שביטויים עם n קטן גם קטנים מq? זה לא מתקיים רק החל מN גדול?

אהלן נווה,

הכוונה כאן היא שבכל פעם שאת רואה n קטן, מדובר באינדקס שגדול מ- N גדול (n>N). 

לכן למשל אם אני רואה a_n, אני מבין שמדובר באיבר בסדרה שמקומו גדול מ- N גדול, הוא יכול להיות a_N+1 למשל או a_N+2 וכו' וכו'.

מקווה שירדת לסוף דעתי,

שתהיה שבת שלום!

אהלן נווה שבוע טוב!

לא, אין כאן שני N-ים שונים.

השתמשתי ב- N גדול כדי לסמן מקום בסדרה כך שהחל ממנו והלאה אי-השוויון לעיל (בתמונה) מתרחש.

ואז השתמשתי באותו N גדול לפירוק הסדרה a_n.

אני מוצא שהדרך הטובה ביותר עבורי להבין פירוקים של מכפלות וסכומים היא פשוט ע"י הצבה פשוטה.

למשל, בפירוק של הסדרה a_n, אני יודע ש- n>N, אז נסה להציב למשל n=N+1, ואז תקבל את השוויון:

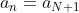
ואם תציב n=N+2, אז תקבל את הפירוק:

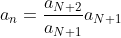
ואם תציב n=N+3, אז תקבל את הפירוק:

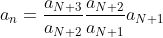
וכך הלאה בצורה זו.

והכוונה היא שהשיוויון הזה נשמר נכון לכל n>N, כלומר הוא נכון ל- n=N+1  ול- n=N+2 ול- n=N+3 וכך הלאה לכל n>N כפי שהדגמנו לעיל.

מקווה שיותר ברור,

אם לא - תמשיך לשאול ללא היסוס.

שפע ברכה והצלחה מאת ה'

חן

בשמחה!

שפע ברכה והצלחה מהשמיים,

חן.